AMORÉ STEYN

Graham Newcater is to our knowledge the only South African composer to have used the twelve-tone system consistently throughout his career. A comparative study of the works in Newcater’s oeuvre indicates that the structures of the various rows he uses have a lot in common. One of the most common characteristics found within these rows is the restriction in the variety of intervals that are used. Newcater rarely uses morc than four types of interval within a row, and he sometimes even limits this numbcr to two. Newcater is also consistent in his choice of intervals. He has a predilection for minor seconds and minor thirds. His rows also often contain major seconds and thirds, as well as the occasional tritone.

Newcater generally avoids using perfect fourths and fifths. In her doctoral thesis, Rörich (1984: 214-216) suggests several possible reasons for Newcater’s choice of interval. First, a smaller range of intervals will allow for greater homogeneity within the work. Secondly, rows that contain a lot of semitones will provide the composer with certain possibilities during composition. For instance, when the respective trichords, tetrachords or hexachords of such rows are re-ordered, chromatic subsets can be revealed. These subsets then allow the composer to freely use chromatic passages while at the same time preserving the link to the original row. The presence of semitones consequendy also allows for the use of major sevenths, minor ninths and semitonal cluster-tetrachords, all of which are combinations often used by Newcater. Despite his respect for both Schoenberg and Berg, Newcater’s use of the twelve-tone row is more similar to that of Anton Webern. Like Webern he sees the row as a source of separable motives rather than a strictly ordered formation. (Rörich 1987: 108) He often makes use of existing rows, mostly those created by Webern, as he considers the rows of Schoenberg and Berg too tonal in their implication. For example, the set used in his violin concerto, trombone concerto, Temple music, Vier Kleine Orchesterliede and Palindromic Structures is taken from Webern’s Variations for Orchestra, op.30 (Ex. 5.1)

For his third symphony Newcater uses yet another Webernian row, the one from the String Quartet op. 28 (Ex. 5.2)

As can be seen in the above examples, the intervallic content of both these Webernian rows is similar to that of the ‘typical’ Newcaterian row. Both rows contain an abundance of semitones and thirds and do not have any tonal references. Newcater often employs the same row for various works, as can be seen in Variations de Timbres, Raka, the Symphony No. 3 and Palindromic Structures. His violin and trombone concertos also have a row in common, as do his Trio, String quartet no. 1 and Threnos. (Rorich 1987: 107).

Another characteristic of Newcater’s compositional approach that he shares with Webern is that he prefers to limit the amount of material he has available to work with. Newcater also often uses one row as the basis for a number of different works. His trio, first string quartet, and Threnos also have a row in common, as do Raka and Variations de Timbres. Newcater’s Symphony No. 1 is his only work that incorporates two different main rows.

Apart from physically limiting the amount of rows he likes to use, Newcater also often employs certain compositional techniques to further minimize the amount of material that is yielded by a row and its permutations. Probably the most common of these techniques is combinatoriality. The design of a combinatorial row is such that it will allow a certain segment of a row to generate its own complementary segment through the process of transposition. For instance, a hexachord from a row with combinatorial properties could be transposed to produce its own complementary hexachord. The original hexachord and the product of its transposition can then be combined to form a new row.

Both the previously mentioned Webernian rows, as well as the second row from Newcater’s Symphony No. 1, are combinatorial. In Example 5. 3, combinatoriality is used to create a new row out of the one shown in Example 5. 1. First, the original first hexachord of the row is transposed an augmented fourth higher. Then this transposition replaces the original second hexachord to form a new row together with the original first hexachord.

Invariance is another technique that is used to limit the available compositional material. Rows with invariant properties will have one or more of their segments present in some of their permutations, thus limiting the amount of new material that is generated by the row permutations and increasing the overall homogeneity. The segments that are duplicated can vary in length, and can encompass anything from three notes to entire rows. In Example 5. 4, the first trichord of the main row is duplicated, albeit in a different order. As illustrated in the matrix, the notes C sharp, F and E flat are also used to make up the first trichord of permutation 14. In this specific example, the first trichord of the prime row is therefore invariant at 14. (Haimo 1990: 184)

Another example of invariance can be seen in the row used for Newcater’s Songs of the Inner Worlds. Apart from the fact that this row is also combinatorial (since the first hexachord can be transposed to produce its complement), its two hexachords are also transposed inversions of each other. This characteristic causes the compositional matrix to yield only 24 possible permutations, as opposed to the usual 48, since PO = RI 1. P1 = R12, etc. This is the most extreme form of invariance, and an effective way to limit the thematic material that is available to the composer. (Ex. 5. 5)

Finally, Newcater occasionally uses derivation in addition to combinatoriality and invariance. A row with derivational qualities is constructed from a single germ cell or small segment. This segment is used to generate all of the various segments of the row, so the result will be a row that is entirely inter-related. Derivation was one of Webern’s favourite ways of creating a new row. A famous example of this technique can be seen in his op. 28, where he uses a single tetrachord (BACH = B flat, A, C, B natural) to generate the main row (Ex. 5. 6). Webern chooses, however, not to start the row on a B flat, but on a C sharp instead. The first and the third tetrachords of the row are exact transpositions of the BACH tetrachord, and the second tetrachord is an inverted transposition of it. This tetrachord therefore dictates the structure of the entire row. (Ex. 5. 7) [Bailey: 24-25] This row also portrays invariant qualities since this row’s second hexachord is identical to the retrogade inverted form of the first hexachord. Therefore this compositional matrix will also only produce 24 permutations, similar to that of Newcater’s Songs of the Inner Worlds.

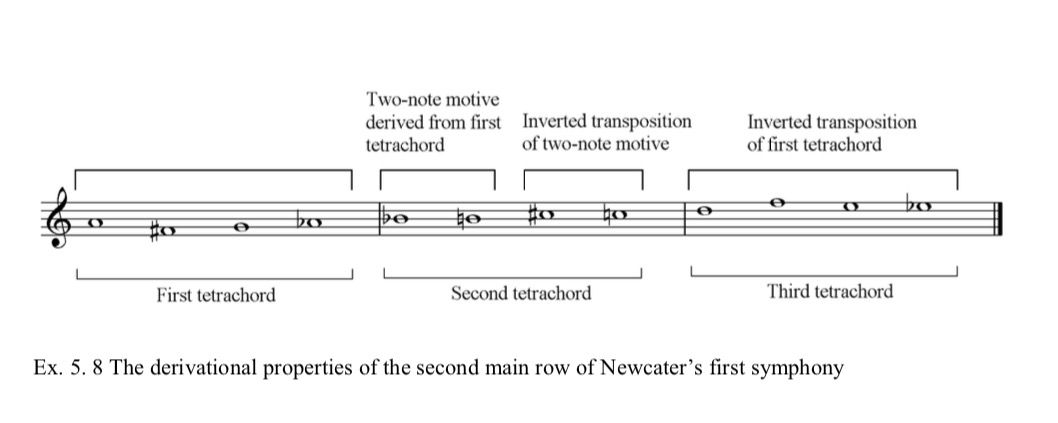
The rows that Newcater borrowed from Webern’s op.28 and op.30 both have derivational qualities. The second row of Newcater’s Symphony No. 1 is an example of one of Newcater’s own rows that portrays this characteristic. As shown in Example 5.8, this entire row of Newcater’s is derived from its own first tetrachord.

The row that Newcater uses in Raka is similar to the other rows he uses in his oeuvre, especially with regard to intervallic content. In its normal form, the Raka row contains six semitones that can be found between consecutive noes, as well as one minor third, three major thirds and one major second interval (Ex. 5. 9). This row does not, however, have any significant derivational, combinatorial or invariant characteristics.

Although the Raka row does not display any clear derivational properties, the four trichords of the Raka row show certain similarities as far as structure is concerned. Three different intervals can be identified in each of the trichords (In this case the relationship between the first and third notes of each trichord should also be taken into consideration). Each trichord contains the same three intervals: a minor second, a major third and a minor third (Ex. 5. 10).

You can download a PDF of Amoré Steyn’s dissertation here.